大学受験・数学塾【掲示板】
区分求積法 - まさ
2020/09/13 (Sun) 12:39:43
いつもありがたくHPを拝見しております。
区分求積法のPDFの1ページ目の下、
k-1番目の四角形の面積となっていますが、
k+1番目ではないでしょうか?
Re: 区分求積法 - 管理人 makoto n.
2020/09/13 (Sun) 23:37:21
いつもご利用ありがとうございます。
確かにご指摘の通り,k+1番目ですね。
修正しておきますので,ご確認ください。
ご指摘ありがとうございました。
新ホームページ - Y
2016/09/05 (Mon) 20:45:52
http://www.uee-math.com/index.html
が新しいホームなんですね
年度ごとの演習問題も復活してください
Re: 新ホームページ - 管理人
2016/09/06 (Tue) 08:55:03
そうです!そのアドレスが新しいホームページです。
年度ごとの演習問題は,演習ルームで分野ごとに分類して復活させる予定です。
今後ともよろしくお願いいたします。
Re: 新ホームページ - tk
2016/11/22 (Tue) 15:30:43
前のURLのリンクが繋がらず一瞬焦りましたが、新ホームページができたのですね^^
これからもこちらのサイトにお世話になると思います。
どうぞよろしくお願いいたします^^
Re: 新ホームページ - 管理人
2016/11/23 (Wed) 09:08:46
以前使用していたサーバーが落ちたまま復旧の目途が立たないようなので,サーバーをリニューアルしたんです!
時間があるときに少しずつ復旧させていく予定ですので,今後もよろしくお願いいたします。
大学受験・数学塾 HPリニューアル情報 - 管理人
2016/08/18 (Thu) 08:49:32
しばらくしたらこの掲示板を閉鎖するつもりでしたが,
今後も引き続き使用することになりました!
今後ともよろしくお願いいたします。
大学受験・数学塾Homepage消失 - Y
2016/08/11 (Thu) 02:09:24
大学受験・数学塾のHomepage消失されているので新しいPageがあれば教えてください. せめてPDFファイルで勉強したいのでPDFの場所だけでも
Re: 大学受験・数学塾Homepage消失 - 管理人
2016/08/11 (Thu) 10:19:00
ご迷惑をおかけして申し訳ありません。
HPを掲載しているサーバー(www42.tok2.com)がダウン
しているようで,ここ2か月間HPにアクセスできない状況です。
下記参照
http://my.7artisan.com/serverstatus.php
復旧の目途が今のところ立っていないようです。
HPの最新の状況は,twitterで呟いています。
ハッシュタグは,#high_mathです。
ご迷惑をおかけしますが,復旧までいましばらくお待ちください。
分数型漸化式について - toshi
2016/02/11 (Thu) 21:58:09
大変ためになるHPをありがとうございます。
ところで、短期集中の漸化式中級編14ページの、
an=2・(1/4)Λn-1 -2 / -2(1/4)Λn-1 -1
が、
2・4Λn-1 -2 /4Λn-1 +2
になる過程がわかりませんので、教えていただけると助かります。よろしくお願いいたします。
Re: 分数型漸化式について - 管理人
2016/02/12 (Fri) 22:11:42
ありがとうございます。
その式変形は,
①分子分母に,4^(n-1)をかける。
②分子分母に,-1をかける。
とすれば得られます。
計算してみてください。
Re: 分数型漸化式について - toshi
2016/02/14 (Sun) 12:27:48
ありがとうございました。
大変よくわかりました!
で 割り切れる の 証明 - ★
2016/01/10 (Sun) 13:11:47
(1) 3^(n + 1) + 4^(2*n - 1)∈13Z
(2) 3^(4*n + 2) + 5^(2*n + 1)∈14Z
なる 2問が 合同式により証明されていますが.
a[n]= 3^(n + 1) + 4^(2*n - 1) が満たす 線型漸化式を つくり 証明願います。
その方法をも pdf に 付記願います。
a[n]= 3^(4*n + 2) + 5^(2*n + 1) が満たす 線型漸化式を つくり 証明願います。
その方法をも pdf に 付記願います。
そうすれば この手法が 世に 蔓延る筈ですので,
Re: で 割り切れる の 証明 - 管理人
2016/02/12 (Fri) 22:13:18
別解の提案ありがとうございます。
すぐに反映できないかもしれませんが,時間があれば記載しようと思います。
漸化式 - ★
2015/03/26 (Thu) 16:54:41
http://www42.tok2.com/home/makoto0614/tokenai-recursion.pdf
を 拝読しました。
>ここで与えられた 数列 の一般項を求めるのは困難です…っていうより求められません
と ありますが 解けて ;
a[n]= (1/5)*((15^(2^(n - 1))) + (10^(2^(n - 1))))/((15^(2^(n - 1))) - (10^(2^(n - 1))))
Re: 漸化式 - 管理人
2015/03/27 (Fri) 09:09:39
ご助言ありがとうございます。
検証して,訂正しておきます。
Re: 漸化式 - 通りすがり
2015/04/23 (Thu) 00:36:39
極限の1番目の問題ですね。
y[n]=(5x[n]-1)/(5x[n]+1) とおくと
y[n+1]=(y[n])^2 が得られるので… の流れで解けてしまいます。
★さんの式は約分できるので、下の形になりますね。
x[n]= (1/5)*((3^(2^(n - 1))) + (2^(2^(n - 1))))/((3^(2^(n - 1))) - (2^(2^(n - 1))))
複素数 - 信濃
2015/02/27 (Fri) 21:59:13
前期試験を受けてきました。静岡大学を受けたのですが,全国的にも珍しく複素数が出題されました。
Re: 複素数 - 管理人
2015/03/02 (Mon) 11:06:15
受験報告ありがとうございます。
確かに,今年の入試はあまり複素数平面は出題されていないようです。新旧課程で共通分野を出題し,出題者の負担を減らしたのでしょうか??
来年以降は,旧課程の移行措置はなくなりますので,複素数平面の出題も増えることが予想されます。
受験生のみなさん!掲示板に受験報告をいただけると後輩や次年度以降の入試情報の参考になるので,どんどん書き込んじゃって下さい♪
2003年岡山大学の問題の略解 - 洋ナシ
2015/01/11 (Sun) 18:58:24
大問4の(3)の答えは(2√2)π(b-a)(ab+1)/3
のような気がします あんまり自信がないですが...
Re: 2003年岡山大学の問題の略解 - 管理人
2015/01/14 (Wed) 08:40:32
略解は、某書の答えをそのまま記載していていましたが、自分で解いてみると確かにその答えになりますね。某書の答えが間違っていたようです。失礼しました。
ご迷惑をおかけしました。訂正しておきます。ありがとうございました。
演習ルームの問題 - R
2014/11/18 (Tue) 20:38:18
2014年度版の演習ルームの問題と解説のファイルですが、第27回からの分がnot foundになってしまいます。
Re: 演習ルームの問題 - 管理人
2014/11/19 (Wed) 10:16:08
ご連絡ありがとうございます。
先日、サーバーがダウンしたようで、その際にファイルが消えてしまったものと思われます。
復旧作業が終わりましたので、ご確認下さい。
ご迷惑をおかけしました。
2007年度30回の整数問題の別解 - IT
2014/10/31 (Fri) 23:24:54
2007年度30回の整数問題はおもしろい問題ですね。
別解を考えましたので、一般性は低いですが投稿します。
p^2 = x^3 + y^3 = (x + y)(x^2-xy+y^2)
x+y≧2なので
(1)x+y=p,x^2-xy+y^2=p、(2)x+y=p^2,x^2-xy+y^2=1 の2通りの可能性がある。
以下x≧yの場合を考える
(1)のとき
x+y=x^2-xy+y^2…(ア)
移項して整理 x(x-y-1)+y(y-1)=0…(イ)
x=yのとき
(ア)より2x=x^2
よってx=2,y=2
x^3+y^3=16となり不適
x>yのとき
(イ)よりx-y-1=0かつy-1=0
よってy=1,x=2
x^3+y^3=9=3^2となり適
(2)のとき
x^2-xy+y^2=x(x-y)+y^2=1
よってx=yかつy=1
x^3+y^3=2となり不適
x^3+y^3はx,yについて対称なのでx<yの場合も同様
よって求めるp,x,yは、p=3,(x,y)=(2,1)、(1,2)
注)x,yが自然数であることは断りなしに使っています。
Re: 2007年度30回の整数問題の別解 - 管理人
2014/11/04 (Tue) 15:49:34
別解の掲載ありがとうございます。
情報交換の場として盛り上がると幸いです。
2012年度25番 - ピカチュウ
2014/11/04 (Tue) 02:46:41
(1)の増減表は間違っていると思うのですが…。
Re: 2012年度25番 - 管理人
2014/11/04 (Tue) 09:36:14
ご指摘ありがとうございます。
確認して修正をしておきます。
2007年度第27回演習別解 - IT
2014/11/01 (Sat) 06:49:43
(3)方針
n-1箇所に 仕切り(+)を入れるか入れないかなので
2^(n-1)通り、そのうち1つも仕切りを入れない場合を除くので、2^(n-1)-1通り。
逆関数のグラフの交点の個数について - IT
2014/10/28 (Tue) 19:49:34
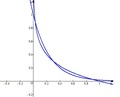 2007年の演習問題の5の(2)で
2007年の演習問題の5の(2)で
y = f(x) とy = f^-1(x) はy = x に関して対称であるから,y = f(x) とy = x がただ1 つの交点を持てばよいい.…(A)... ゆえに,a<0 , a =1/e としておられますが、例えばa=-4のときy = f(x) とy = f^-1(x)は3つの交点を持ちます。(別図)
a=-eが境界になると思います。
例えば、
y=-xの逆関数がy=-x
y=1/x の逆関数がy=1/x であることなどからも、
(A)が誤りであることが分かります。
Re: 逆関数のグラフの交点の個数について - 管理人
2014/10/29 (Wed) 00:02:31
おっしゃる通りですね。
ご指摘ありがとうございました。近日中に,ファイルを修正しておきます。
テスト最中の計算の見直しについて - ぷー
2014/08/11 (Mon) 22:10:34
HP拝見しました。
わからない問題を調べていて偶然見つけたサイトなのですが参考になることばかりでとても重宝しています!!
突然なのですが僕は数学が大好きなのですが、センター試験の数学が苦手です。
たまに自分の出した答えと空欄の形が合わなくて、何度も自分の計算を見直すのですけれども、テストの時間内に間違った箇所がなかなか見つからなくて自爆することがたまにあります。
こういったことを防ぐにはどういうことを意識して試験に挑めばいいでしょうか?また、普段どういうことを意識して勉強すればいいでしょうか?
アドバイスがあればよろしくお願いします。
Re: テスト最中の計算の見直しについて - makoto@管理人
2014/08/12 (Tue) 18:51:50
センター試験の数学において計算間違いは致命傷になるので、同じような悩みを持っている人も多いと思います。
限られた時間内に早く正確に計算することは簡単なことではありませんが、ある程度対策の方法はあります。
1.途中で見直しができるように計算はあちこちにしない。
限られたスペースで計算をするので、あちこちに計算する
人がいますが、これではいざ見直しをするときや計算間違
いが発覚したときにどこで間違えたのかわかりません。
自分なりのルールに基づいて計算する場所の順序は決めて
おきましょう。
2.数字や記号(特に+-などの符号)は適当に書かず丁寧に
かく。
計算間違いの多くは、写し間違いや勘違いから起こりま
す。上の行では+だったのに次の行で-になったり、展開
したときに符号を間違えたりするケースです。間違いを探
すときは、このような場所から探すと良いのではないで
しょうか?
3.検算ができるなら検算をする。
数列などは、一般項が出た時点でn=1,2,…などを代入して
問題文の条件にあうかどうか検算ができます。数列に限ら
ず関数の問題でもx=0,1,2などを代入してある程度検算で
きるものがあります。答えが合っているかどうか簡単に確
認できるものに関しては確認をした方がよいでしょう。
普段から検算を意識することは大切です。出てきた答えが妥当な数値なのか?(図形問題なら三角形の成立条件を満たしているか?など)を考えることでおかしなことに気付くこともあります。
私は、普段から生徒にセンターの点数を上げる手っ取り早い方法は、ミスをなくすことだ!と言っています。人間なのでミスはありますから、それをできるだけ少なくできるようにすることが大切だと言っています。高3生ならこれから模試のシーズンを迎えます。ミスを減らして、実力が出し切れることを祈っています。
Re: テスト最中の計算の見直しについて - ぷー
2014/08/12 (Tue) 23:44:13
思っていたより早くお返事が返ってきて感激です!
アドバイス頂いた事を参考にして次のテストに活かしたいです!
センターでなくとも数学の試験は時間が限られているので最後は残った時間で計算に詰まった問題に手を出すか、解き方のわからない問題をもう少し粘ってみるかその決断でいつも葛藤します。後でもっとこうできたはずだと後悔することも沢山あります。
いろいろテストには思い悩むこともあるのですけれどもアドバイスを頂いてとても元気が出ました。いい結果が出るように頑張ります!
Re: テスト最中の計算の見直しについて - makoto@管理人
2014/08/13 (Wed) 00:41:44
元気が出ただけでも良かったです。
アドバイスが実際に役に立てばなお嬉しいですね。
確かに、限られた時間で計算に詰まった問題と解き方の分からない問題とどちらに手を出すのが正解かは難しいですよね。
採点基準によってかなり違うので一概に言えませんが、『方針点』というものも存在します。計算の過程が間違っていたとしても方針が合っていればある程度の点数を与えるというものです。全く解き方が分からない問題でもある程度の方針が立ったのであれば、少し書いてみるのも良いかもしれません。最も方針が違えば0点になりますが…
計算に詰まった問題は、符号のミスや勘違いなどが原因であることが多いと思うので、それを修正できれば確実に得点につながるという意味ではこちらの方が得点になるかもしれませんね!
Re: テスト最中の計算の見直しについて - ぷー
2014/08/13 (Wed) 22:36:24
帰ってきてドキドキしながらパソコンを立ちあげてみたら返信があって、嬉しくてまた返事してしまいました。
「方針点」があるんですね。僕ももうすうすは何となく感じていたのですがそれも加味して作戦を立てたいです。
最近なかなか勉強すれども点数が伸びなくて、恥ずかしくて周りにも相談できなくて思い悩んで勉強が手に付かないこともあったのですけれどもこうして掲示板に書き込んでアドバイスを頂けてホントに元気が出ました。ありがとうございます。
そして、今日は今から問題解きなおして単語帳読み返して寝ます!
2013年度の演習問題がなくなっているようですが - 通りすがり
2014/02/11 (Tue) 15:40:15
2013年度の演習問題がなくなっているようですが。
Re: 2013年度の演習問題がなくなっているようですが - makoto(管理人)
2014/02/11 (Tue) 15:43:20
どの演習問題がなくなっていますか?
ページ自体は存在していますので,ページの更新をしてみてください.
無題 - あおい
2014/01/20 (Mon) 14:07:44
演習ルームの2013年の問題の、2009年筑波大学の(1)の解答ですが、
うち間違えだと思われますが、cos3θ=4cos3θ-3cosθとなってますが、4cos^3θですよね?
Re: 無題 - マコト@管理人
2014/01/21 (Tue) 01:58:32
報告ありがとうございます!
入力ミスですね.
訂正しておきます.
ありがとうございました.
今後ともよろしくお願いいたします
無題 - ゆみ
2013/09/29 (Sun) 21:31:25
お久しぶりです。
突然ですが、次数についておしえてください。
最高次数の問題をしていて、分からなくなりました・・・
Re: 無題 - マコト
2013/09/30 (Mon) 01:16:51
次数とは,単項式(掛け算で表されている式)において掛けている文字の個数を言います.
例えば,x^2y^3であれば,xについては2次で,yについては3次となります.また,x,yについては5次になります.
多項式で言うと,各項で最も次数が高いものがその多項式の次数となります.
例えば,x^3+2x-2は,
x^3が3次,2xが1次,-2は定数項
なので,最も次数が高いのは3ですから,この式の次数は3となります.
積分の問題で出てくる最高次数の問題をやっているのでしょか?左辺と右辺の最高次数を考えればよいです.
無題 - ゆみ
2013/07/26 (Fri) 22:54:54
まことさんごめんなさい
また初歩的な質問をします。
eloge はいくつですか?
ど忘れしてしまって・・・(泣)
あと、できれば固有値固有ベクトルについての
演習問題を作って頂きたいです。
Re: 無題 - makoto@管理人
2013/07/27 (Sat) 08:02:43
log e=1 なので,elog e=e となります.
固有値と固有ベクトルについての演習問題ですが,現在夏期講習中で余裕がないため,申し訳ないですがすぐにというわけにはいきません.ご了承下さい.9月以降余裕があれば円周ルームで扱うかもしれません.
無題 - ゆみ
2013/07/27 (Sat) 21:24:13
ありがとうございました。
たまにふっと忘れてしまうんです・・・
演習問題の件も了解しました。
夏期講習中にも関わらずありがとうございました
無題 - ひろ
2013/07/23 (Tue) 18:40:53
ベクトルの終点の存在範囲がいまいちわからないのですが、どうすればいいですか・・・ アバウトすぎてごめんなさい・・・
